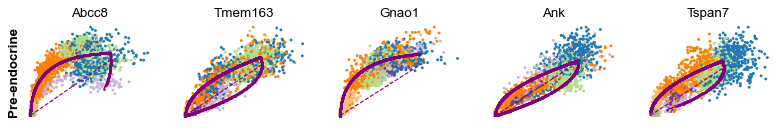Dynamical Modeling

Here, we use the generalized dynamical model to solve the full transcriptional dynamics.

That yields several additional insights such as latent time and identification of putative driver genes.

As in the previous tutorial, it is illustratively applied to endocrine development in the pancreas.

# update to the latest version, if not done yet.
!pip install scvelo --upgrade --quiet

import scvelo as scv
scv.logging.print_version()

Running scvelo 0.2.0 (python 3.8.2) on 2020-05-15 00:27.

scv.settings.verbosity = 3  # show errors(0), warnings(1), info(2), hints(3)
scv.settings.presenter_view = True  # set max width size for presenter view
scv.settings.set_figure_params('scvelo')  # for beautified visualization

Prepare the Data

Processing consists of gene selection, normalizing by total size, logarithmizing X, and computing moments for velocity estimation. See the previous tutorial for further explanation.

adata = scv.datasets.pancreas()

scv.pp.filter_and_normalize(adata, min_shared_counts=20, n_top_genes=2000)
scv.pp.moments(adata, n_pcs=30, n_neighbors=30)

Filtered out 20801 genes that are detected in less than 20 counts (shared).
Normalized count data: X, spliced, unspliced.
Logarithmized X.
computing neighbors
    finished (0:00:03) --> added
    'distances' and 'connectivities', weighted adjacency matrices (adata.obsp)
computing moments based on connectivities
    finished (0:00:00) --> added
    'Ms' and 'Mu', moments of spliced/unspliced abundances (adata.layers)

Dynamical Model

We run the dynamical model to learn the full transcriptional dynamics of splicing kinetics.

It is solved in a likelihood-based expectation-maximization framework, by iteratively estimating the parameters of reaction rates and latent cell-specific variables, i.e. transcriptional state and cell-internal latent time. It thereby aims to learn the unspliced/spliced phase trajectory for each gene.

scv.tl.recover_dynamics(adata)

recovering dynamics
    finished (0:13:31) --> added
    'fit_pars', fitted parameters for splicing dynamics (adata.var)

scv.tl.velocity(adata, mode='dynamical')
scv.tl.velocity_graph(adata)

computing velocities
    finished (0:00:04) --> added
    'velocity', velocity vectors for each individual cell (adata.layers)
computing velocity graph
    finished (0:00:08) --> added
    'velocity_graph', sparse matrix with cosine correlations (adata.uns)

Running the dynamical model can take a while. Hence, you may want to store the results for re-use, with adata.write('data/pancreas.h5ad', which can later be read with adata = scv.read('data/pancreas.h5ad').

#adata.write('data/pancreas.h5ad', compression='gzip')
#adata = scv.read('data/pancreas.h5ad')

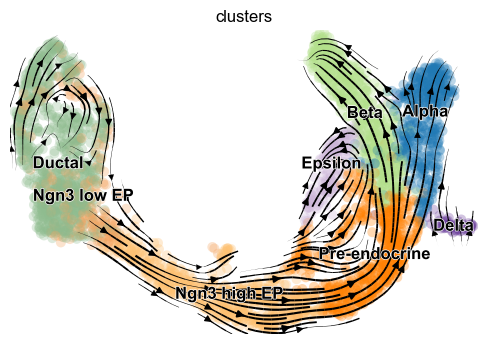
scv.pl.velocity_embedding_stream(adata, basis='umap')

computing velocity embedding
    finished (0:00:00) --> added
    'velocity_umap', embedded velocity vectors (adata.obsm)

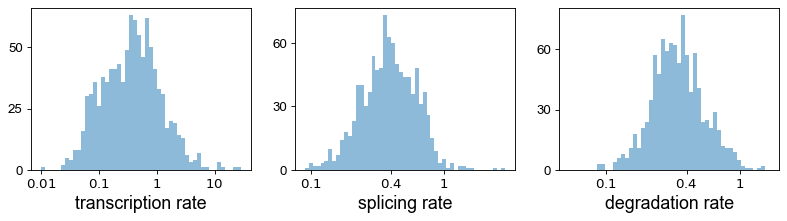
Kinetic rate paramters

The rates of RNA transcription, splicing and degradation are estimated without the need of any experimental data.

They can be useful to better understand the cell identity and phenotypic heterogeneity.

df = adata.var
df = df[(df['fit_likelihood'] > .1) & df['velocity_genes'] == True]

kwargs = dict(xscale='log', fontsize=16)
with scv.GridSpec(ncols=3) as pl:
    pl.hist(df['fit_alpha'], xlabel='transcription rate', **kwargs)
    pl.hist(df['fit_beta'] * df['fit_scaling'], xlabel='splicing rate', xticks=[.1, .4, 1], **kwargs)
    pl.hist(df['fit_gamma'], xlabel='degradation rate', xticks=[.1, .4, 1], **kwargs)

scv.get_df(adata, 'fit*', dropna=True).head()

	fit_r2	fit_alpha	fit_beta	fit_gamma	fit_t_	fit_scaling	fit_std_u	fit_std_s	fit_likelihood	fit_u0	fit_s0	fit_pval_steady	fit_steady_u	fit_steady_s	fit_variance	fit_alignment_scaling
index
Sntg1	0.401981	0.015726	0.005592	0.088792	23.404254	42.849447	1.029644	0.030838	0.406523	0.0	0.0	0.159472	2.470675	0.094304	0.149138	5.355590
Sbspon	0.624803	0.464865	2.437113	0.379645	3.785993	0.154771	0.058587	0.178859	0.252135	0.0	0.0	0.182088	0.164805	0.430623	0.674312	1.193015
Mcm3	0.292389	3.096367	39.995796	0.638543	2.049463	0.013943	0.016253	0.673142	0.228207	0.0	0.0	0.467683	0.051432	1.927742	0.687468	0.887607
Fam135a	0.384662	0.172335	0.118088	0.204538	11.239574	1.124040	0.356525	0.149868	0.283343	0.0	0.0	0.387921	1.345830	0.393197	0.671096	3.390194
Adgrb3	0.384552	0.046828	0.006750	0.196856	6.992542	71.850736	2.153206	0.030417	0.250195	0.0	0.0	0.068851	5.214500	0.093570	0.556878	1.893389

The estimated gene-specific parameters comprise rates of transription (fit_alpha), splicing (fit_beta), degradation (fit_gamma), switching time point (fit_t_), a scaling parameter to adjust for under-represented unspliced reads (fit_scaling), standard deviation of unspliced and spliced reads (fit_std_u, fit_std_s), the gene likelihood (fit_likelihood), inferred steady-state levels (fit_steady_u, fit_steady_s) with their corresponding p-values (fit_pval_steady_u, fit_pval_steady_s), the overall model variance (fit_variance), and a scaling factor to align the gene-wise latent times to a universal, gene-shared latent time (fit_alignment_scaling).

Latent time

The dynamical model recovers the latent time of the underlying cellular processes. This latent time represents the cell’s internal clock and approximates the real time experienced by cells as they differentiate, based only on its transcriptional dynamics.

scv.tl.latent_time(adata)
scv.pl.scatter(adata, color='latent_time', color_map='gnuplot', size=80)

computing terminal states
    identified 2 regions of root cells and 1 region of end points
    finished (0:00:00) --> added
    'root_cells', root cells of Markov diffusion process (adata.obs)
    'end_points', end points of Markov diffusion process (adata.obs)
computing latent time
    finished (0:00:02) --> added
    'latent_time', shared time (adata.obs)

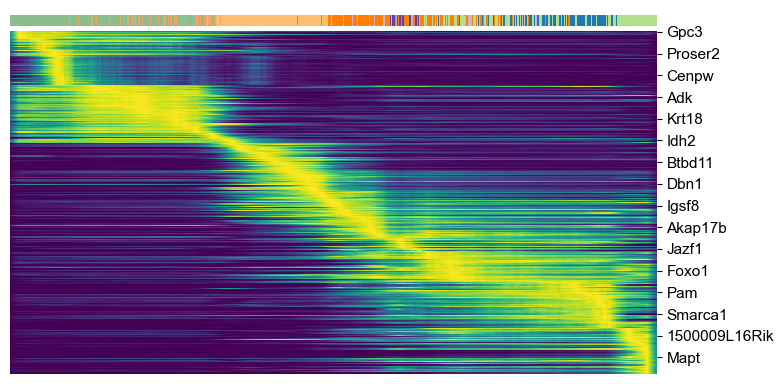
top_genes = adata.var['fit_likelihood'].sort_values(ascending=False).index[:300]
scv.pl.heatmap(adata, var_names=top_genes, sortby='latent_time', col_color='clusters', n_convolve=100)

Top-likelihood genes

Driver genes display pronounced dynamic behavior and are systematically detected via their characterization by high likelihoods in the dynamic model.

top_genes = adata.var['fit_likelihood'].sort_values(ascending=False).index
scv.pl.scatter(adata, basis=top_genes[:15], ncols=5, frameon=False)

var_names = ['Actn4', 'Ppp3ca', 'Cpe', 'Nnat']
scv.pl.scatter(adata, var_names, frameon=False)
scv.pl.scatter(adata, x='latent_time', y=var_names, frameon=False)

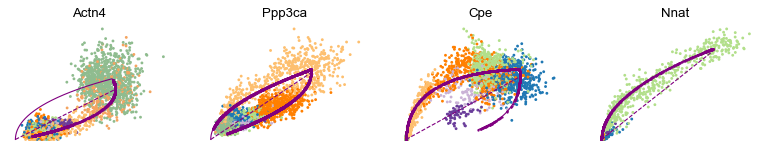
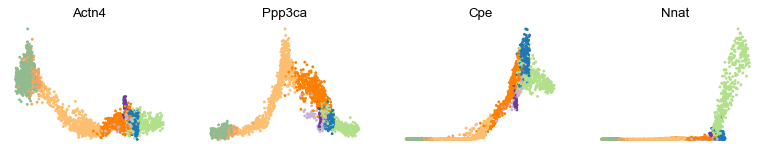
Cluster-specific top-likelihood genes

Moreover, partial gene likelihoods can be computed for a each cluster of cells to enable cluster-specific identification of potential drivers.

scv.tl.rank_dynamical_genes(adata, groupby='clusters')
df = scv.get_df(adata, 'rank_dynamical_genes/names')
df.head(5)

ranking genes by cluster-specific likelihoods
    finished (0:00:03) --> added
    'rank_dynamical_genes', sorted scores by group ids (adata.uns)

	Ductal	Ngn3 low EP	Ngn3 high EP	Pre-endocrine	Beta	Alpha	Delta	Epsilon
0	Dcdc2a	Dcdc2a	Rbfox3	Abcc8	Pcsk2	Cpe	Pcsk2	Tox3
1	Top2a	Adk	Mapre3	Tmem163	Ank	Gnao1	Rap1b	Rnf130
2	Nfib	Mki67	Btbd17	Gnao1	Tmem163	Pak3	Pak3	Meis2
3	Wfdc15b	Rap1gap2	Sulf2	Ank	Tspan7	Pim2	Abcc8	Adk
4	Cdk1	Top2a	Tcp11	Tspan7	Map1b	Map1b	Klhl32	Rap1gap2

for cluster in ['Ductal', 'Ngn3 high EP', 'Pre-endocrine', 'Beta']:
    scv.pl.scatter(adata, df[cluster][:5], ylabel=cluster, frameon=False)